Остойчивость корабля, способность его плавать на воде в прямом положении и возвращаться в него после прекращения действия внешней причины, изменившей первоначальное положение равновесия судна.

Различают поперечную Остойчивость корабля — при наклонениях вокруг продольной оси корабля и продольную Остойчивость корабля — при наклонениях вокруг поперечной его оси.

Для практики наибольшее значение имеет первая.

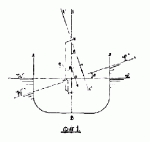
Мерою поперечной Остойчивости корабля служит величина плеча Остойчивости, — перпендикуляра GK (фиг. 1), опущенного из центра тяжести судна G на линию поддержания, т.-е. вертикаль, восстановленную из центра величины корабля C? (см. Водоизмещение) при наклонении его на угол ? (фиг. 1). Часто также мерою Остойчивость корабля называют произведение веса судна P на плечо Остойчивости корабля, т.-е. момент M=P?GK; Плечо Остойчивости корабля при данном угле крена зависит от величины MG, называемой метацентрической высотой и характеризующей отстояние метацентра M (пересечения линий CX и C?x?) от центра тяжести корабля G.

Ясно, что OR=(S—a) Sin?, а момент остойчивости M=p(S—a) Sin?, где S — метацентрический радиус (отстояние метацентра от центра величины), и a возвышение центра тяжести над центром величины.

Остойчивость корабля судна тем больше, чем больше S и меньше a, т.-е. чем выше метацентр и ниже центр тяжести. Характеристикой Остойчивости корабля обыкновенно является метацентрическая высота MG, каковая для современных линейных кораблей составляет 4—6 фт., для миноносцев 2—3 фт.; для мониторов она достигала 12 фт., а у мелких пароходов спускалась до 1—2 фт.

Величина метацентрического радиуса S зависит только от формы и обводов судна и равняется I/v, где I есть момент инерции площади грузов. WL относительно её продольной оси, а V — объём подводной части корабля; т. к. в I ординаты груз. WL входят в кубе, то естественно огромное значение для остойчивости корабля ширины обводов WL.

С уменьшением площади последней, например, при затоплении бортовых отсеков водою (см. Боевая остойчивость корабля), Остойчивость корабля падает с чрезвычайной быстротой. В подвод. судах груз. WL нет, почему Остойчивость корабля их зависит только от положения центра тяжести под центр величины; при обратном размещении этих центров подводное судно перевернется, а при совпадении их (шар) — будет иметь безразличное равновесие.

Но как только подводное судно начинает всплывать, условия его Остойчивость корабля меняются: появляется WL, площадь её быстро увеличивается, и S = I/v делается положительным, как того требует условие Остойчивость корабля для всякого надводного судна. Величина a (отстояние центра тяжести от центра величины), входящая также в формулу Остойчивость корабля, зависит только от нагрузки корабля и определяется подсчетом или практически путем накренивания судна (см. ниже).

Всякое вертикальное перенесение грузов на корабле отражается на a, а следовательно, и на Остойчивость корабля; величина изменения момента Остойчивости корабля от подобных перемещений грузов легко определяется по известной в механике теореме моментов. Добавление или снятие грузов, затопление или осушение различных отсеков на корабле также отражаются на Остойчивость корабля в ту или другую сторону, смотря по положению центра тяжести этих грузов относительно общего центра тяжести судна.

На военных судах обыкновенно наперед рассчитывается, какое влияние на Остойчивости корабля дает заполнение водою каждого значительного отсека. Для теоретического вычисления Остойчивости корабля при значительных углах крена приходится принимать во внимание неравенство объёмов бортовых клиньев — LOL?, входящего в воду (фиг. 1), и WOW?, выходящего из неё, вследствие не симметрии бортов, особенно заметной, когда в воду начнет входить кромка верхней палубы; действующая в-линия W?l? исправляется соответственно разности этих объёмов, после чего вычисляют момент инерции её площади и находят S. Когда верхняя палуба входит в воду, площадь, а с нею и момент инерции I груз. WL сразу значительно уменьшаются, почему Остойчивость корабля резко падает; из-за этого высокобортные суда оказываются много безопаснее низкобортных. Практически Остойчивость корабля определяется накрениванием корабля на тихой воде путем перенесения на палубе его груза M (около 1% от водоизмещения) с борта на борт на расстояние S.

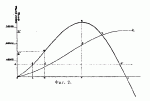
Заметив при этом угол крена ? и зная, что кренящий момент равен выпрямляющему моменту Остойчивость корабля, имеем: m. S = M = P (S — a) Sin? = P. GK; отсюда уже находится мера Остойчивость корабля, т.-е. GK. Найдя вычислением S, определяют попутно a = (S. Sin? — GK)/Sin?, т. е. возвышение центра тяжести корабля над его ценра величины. Подобные опыты накренивания судна производят последовательно несколько раз на один и на другой борт и выводят средний результат всех наблюдений. Наглядное представление об изменении Остойчивости корабля при разных углах крена дает т. наз. диаграмма Остойчивость корабля, предложенная впервые английским инженером Ридом (Read, фиг. 2); для построения её, по горизонтальной оси откладывают углы крена, а по вертикальной — соответствующие плечи, или моменты Остойчивости корабля.

Кривая Рида Obyb’d дает возможность найти угол крена, при котором наступает равновесие корабля, если на него действует постоянная кренящая пара; отложив Oa, равную в масштабе моменту этой пары, из точки a проводят горизонтальную прямую, которая пересечет кривую Рида в точке b; проведя ординату bc, мы в c отсчитаем искомый угол крена; часть кривой над линией abb’ представил собою диаграмму Рида для корабля, когда он имеет этот крен (вследствие, напр., пробоины). Предельная величина кренящей пары представляется длиною yx; если на корабль подействует пара с моментом еще большим, то он опрокинется.

Точка d пересечения кривой с горизонтальной осью показывает, при каком угле крена судно совершенно теряет Остойчивость корабля; чем дальше d от o, т.-е. чем длиннее диаграмма, тем запас Остойчивость корабля больше; конечно, этот запас зависит также и от высоты диаграммы.

На практике нередко приходится иметь дело с кренящими парами, внезапно приложенными к судну (напр., шквал); под влиянием такой пары судно начинает крениться, приобретает некоторую угловую скорость, все увеличивающуюся, пока кренящая пара остается больше выпрямляющей. Корабль придет в положение равновесия, когда моменты обеих пар сравняются; вследствие накопленной угловой скорости (инерции) судно перейдет это положение равновесия и будет крениться дальше, но при этом выпрямляющая пара станет уже больше кренящей, угловая скорость судна будет постепенно уменьшаться, и корабль остановится. После этого он начнет возвращаться в положение равновесия, снова его перейдет и, т. обр., будет качаться подобно маятнику (см. Качка). Важно уметь определять тот угол, до которого внезапно приложенная пара накренит корабль; этот угол настолько лежит за положением равновесия, что избыток работы выпрямляющей пары над работою кренящей, при наклонении корабля от положения равновесия до этого угла, равен избытку работы кренящей пары над работою, выпрямляющей при наклонении от нуля до положения равновесия.

Из механики известно, что работа кренящей пары, с моментом M=oa, графически изображается площадью прямоугольника со сторонами: Oa — равной моменту пары и Oc — равного соответствующему углу поворота; работа же выпрямляющей пары, меняющаяся согласно кривой Рида, изображается площадью, заключенной между кривой и горизонт. осью в пределах соответствующих ординат.

Вышеупомянутый избыток работы кренящей пары над выпрямляющей изобразится площадью: oabc—obc=oab, а избыток работы выпрямляемой пары над кренящей во 2-й период качания — площадью: cbnek—cblk=bnl. Чтобы определить угол, до которого корабль накренится под влиянием внезапно приложенной кренящей пары, надо найти на диаграмма Рида такую ординату nk, чтобы площадь obc=площ. ?bnl; отрезок ok даст искомый угол, тогда как Oc дает угол, при котором наступит равновесие кренящего и выпрямляющего моментов. Работа выпрямляющей пары при наклонении корабля от прямого положения называется динамической Остойчивости корабля. Графически она выражается на фиг. 2 кривою oprs, ординаты коей представляют величины работы выпрямляющей пары при соответствующих углах крена.

Динамическая Остойчивость корабля особенно важна для парусных судов, т. к. только по ней можно судить о способности корабля сопротивляться действию шквала; нельзя в этом случае ограничиваться суждением по величине плеча статической Остойчивости корабля, каковое м. быть еще значительным в момент, когда судно уже переворачивается из-за недостатка динамической Остойчивости корабля.

Классическим примером сему является гибель в 1870 г. английского военного корабля Captain: идя в эскадре адмирала Мильна под парусами и имея крен 14°, корабль этот неожиданно перевернулся от налетевшего шквала, тогда как остальные суда, и в том числе Monarch, тех же самых размерений и водоизмещения, как Captain, благополучно выдержали шквал.

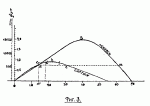
Фиг. 3 изображает диаграммы Рида для обоих этих судов в том же масштабе; из неё видно, что хотя плечо статической Остойчивости корабля Captain при 14° крена было не менее, чем у Monarch, но запас динамической Остойчивости корабля первого, изображаемый площадью abc, составлял всего 400 тонно-фут, тогда как для Monarch он был 6000 тонно-фт. (площ. aBm); поэтому достаточно было небольшого шквала, представляемого линией ae, чтобы опрокинуть Captain, т. к. ? acd оказался уже больше площадки dbf; между тем, шквал той же силы (ок. 9 баллов) наклонил Monarch только до 18° и катастрофы не м. произойти.